 |
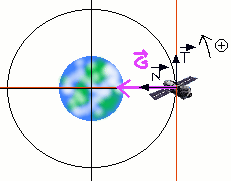
Les conditions d'apesanteur
|
Relation entre G en a |
|
|
  |
|
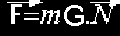 |
|
 |
|
 |
|
 |
|
 |
|
|
|
 |
Les conditions d'apesanteur
|
Relation entre G en a |
|
|
  |
|
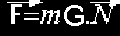 |
|
 |
|
 |
|
 |
|
 |
|
|
|